Рекуррент харьцаа ба матриц
Рекуррент харьцаагаар өгөгдсөн шугаман тэгшитгэлийг/ F(n) = A*F(n-1) + B*F(n-2) / бид нар бодохдоо динамик програмчлалын арга ашиглаж боддог.
int F(int A,int B, int N){
vector< int > F[N+1];
F[1] = 1;
F[2] = 2;
for (int i=3; i<=N;){
F[i] = A*F[i-1] + B*F[i-2];
}
return F[N];
}Энэ нь N-р гишүүнийг олоход O(N) хугацаа зарцуулдаг. Гэвч зарим тохиолдолд бид LogN-р бодох шаардлага гарч ирдэг.
Бид нар шугаман рекуррент тэгшитгэлийг X(i+1) = M X(i) хэлбэртэй бичиж болно.
Үүнд:
X(i+1) болон X(i) нь 1 x K хэмжээтэй матриц. M нь K x Kхэмжээтэй матриц.
| f(n+1) | | f(n) |
| f(n) | | f(n-1) |
| f(n-1) | = M x | f(n-2) |
| ...... | | ...... |
| f(n-k+1) | | f(n-k) |
Эндээс бид нар рекуррент харьцаагаа ашиглаад M матрицаа олно.
1. Хамгийн энгийн рекуррент харьцаа болох Фиббоначийн дараалалыг авч үзье.
f(n) = f(n-1) + f(n-2) => f(n+1) = f(n) + f(n-1) ингэж бичиж болно.
Тэгвэл X(i+1) болон X(i) матрицууд дараах байдлаар бичигдэнэ.
| f(n+1) | = M x | f(n) | => | f(n+1) | = | a b | x | f(n) |
| f(n) | | f(n-1) | | f(n) | | c d | | f(n-1) |
Эндээс харахад бидний K тоо буюу матрицын хэмжээ нь тухайн харьцаа өөрөөсөө өмнөх хэдэн гишүүнээсээ хамааралтай байна гэдгээс олж болох нь харагдаж байна. Фиббаночийн хувьд өмнөх 2 гишүүнээсээ хамаардаг тул матрицын хэмжээ K=2.
Одоо М матрицыг олъё. Дээрх M болон X(i-1) матрицыг үржвэл:
a*f(n) + b*f(n-1) = f(n+1)
c*f(n) + d*f(n-1) = f(n)
Фиббоначийн дараалалын эхний 3-н гишүүнийг мэдэх учир орлуулаад a=1, b=1, c=1, d=0 гэж гарна. Одоо бид М-г мэдэх учраас дараах байдлаар бичиж болно.
| f(n+1) | = | 1 1 | x | f(n) |
| f(n) | | 1 0 | | f(n-1) |
| ? | = | 1 1 | x | 8 |
| 8 | | 1 0 | | 5 |
? => 8*1 + 5*1 = 13

2. f(n) = a * f(n-1) + c * f(n-3) + d * f(n-4) + e тэгшитгэлийн хувьд марицыг олъё.
| a 0 c d 1 | | f(n) | | f(n+1) |
| 1 0 0 0 0 | | f(n-1) | | f(n) |
| 0 1 0 0 0 | x | f(n-2) | | f(n-1) |
| 0 0 1 0 0 | | f(n-3) | | f(n-2) |
| 0 0 0 0 1 | | c | | c |
Анализ
Дараах рекуррентийн хувьд авч үзье: f(n) = f(n-1) + f(n-2).
M x | f(n) | = | f(n+1) |
| f(n-1) | | f(n) |
Тэгшитгэлийн 2 талыг M-р үржье
M x M x | f(n) | = M x | f(n+1) | = | f(n+2) |
| f(n-1) | | f(n) | | f(n+1) |
Эмхэтгэвэл:
M^2 x | f(n) | = | f(n+2) |
| f(n-1) | | f(n+1) |
Дараах байдалтай болох нь харагдаж байна.
M^3 x | f(n) | = | f(n+3) |
| f(n-1) | | f(n+2) |
M^4 x | f(n) | = | f(n+4) |
| f(n-1) | | f(n+3) |
...............................
...............................
...............................
M^k x | f(n) | = | f(n+k) |
| f(n-1) | |f(n+k-1)|
X(i+k) = M^k * X(i) Бид нар 2 матрицыг O(N^3)-д үржнэ.
const Matrix Matrix::operator*(const Matrix &A){
Matrix C(A.N);
for( int i = 0; i < A.N; ++i )
for( int j = 0; j < A.N; ++j ){
for( int k = 0; k < A.N; ++k )
C.data[i][j] = (C.data[i][j] + data[i][k] * A.data[k][j])%MOD;
}
return C;
}Тэгвэл К зэргийг шугаман олвол O(N^3*K).
int naive_power(int a, int k):
int res = 1;
for (int i=1; i<=k; i++){
res *= a
}
return res;Хэрвээ К зэргийг Log-д олж чадвал O(N^3*LogK) болно.
Хуваагаад нэгтгэх аргаар зэргийг O(LogN)-д олох.
2^5-г дараах байдалтай задлая.
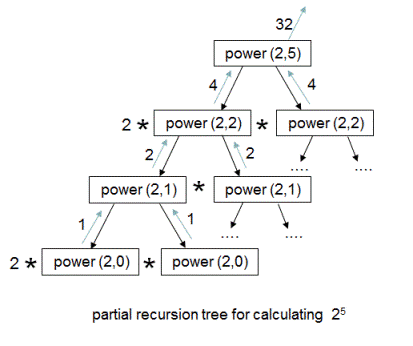
Эндээс дараах байдалтай харагдана.

Хугацааны үнэлгээ нь модны өндөртэй тэнцүү.

int power(int n, int k){
if(k==0)return 1;
if(k==1)return n;
int tmp = power(n, k/2);
if(k & 1)
return tmp*tmp*n;
else
return tmp*tmp;
}int ipow(int base, int exp){
int result = 1;
while (exp){
if (exp & 1)
result *= base;
exp >>= 1;
base *= base;
}
return result;
}Матрицын C++ хэл дээрх код
#include <vector>
#include <iostream>
int MOD = 1000000007;
using namespace std;
class Matrix{
public:
int N;
vector< vector< long long > > data;
Matrix(int N);
Matrix(const Matrix &matrix);
const Matrix &operator=(const Matrix &A);
const Matrix operator*(const Matrix &A);
const Matrix operator^(int P );
~Matrix();
};
Matrix::Matrix(int N){
this->N = N;
data = vector< vector< long long > >(N, vector< long long >(N));
}
Matrix::Matrix(const Matrix &A){
this->N = A.N;
data = vector< vector< long long > >(A.data);
}
Matrix::~Matrix(){
data.clear();
}
const Matrix &Matrix::operator=(const Matrix &A){
if( &A != this ){
data.clear();
N = A.N;
data = vector< vector< long long > >(A.data);
}
return *this;
}
const Matrix Matrix::operator*(const Matrix &A){
Matrix C(A.N);
for( int i = 0; i < A.N; ++i )
for( int j = 0; j < A.N; ++j ){
for( int k = 0; k < A.N; ++k )
C.data[i][j] = (C.data[i][j] + data[i][k] * A.data[k][j])%MOD;
}
return C;
}
const Matrix Matrix::operator^(int P){
if(P == 1) return (*this);
if(P & 1) return ((*this) * ((*this) ^ (P-1)));
Matrix B = ((*this) ^ (P/2));
return (B*B);
}
long long value(Matrix &matrix,int P,vector< int > &def){
if (P <= def.size())
return def[P-1];
Matrix res = matrix^(P-def.size());
int val = 0;
for (int i=0,t = def.size()-1; i<res.data[0].size(); i++,t--){
val = (val + (res.data[0][i] * def[t])%MOD)%MOD;
}
return val;
}
int main(){
vector< int > def = {4,14};
Matrix matrix(2);
matrix.data[0][0] = 3; matrix.data[0][1] = 2;
matrix.data[1][0] = 1; matrix.data[1][1] = 0;
int t;
cin>>t;
while (t--){
int n;
cin>>n;
cout<<value(matrix,n,def)<<endl;
}
return 0;
}